井出 哲(地球惑星科学専攻 教授)
グレゴリー C. べローザ(米国スタンフォード大学 教授)
発表のポイント
- スロー地震とファスト地震(普通の地震)の違いについて、より完全な解釈を提供した。
- 普通の地震こそが、実は特異な現象であるという視点の転換を迫る。
- 地震現象のより正確な物理学的理解により、将来の地震活動予測モデル改善への貢献が期待される。
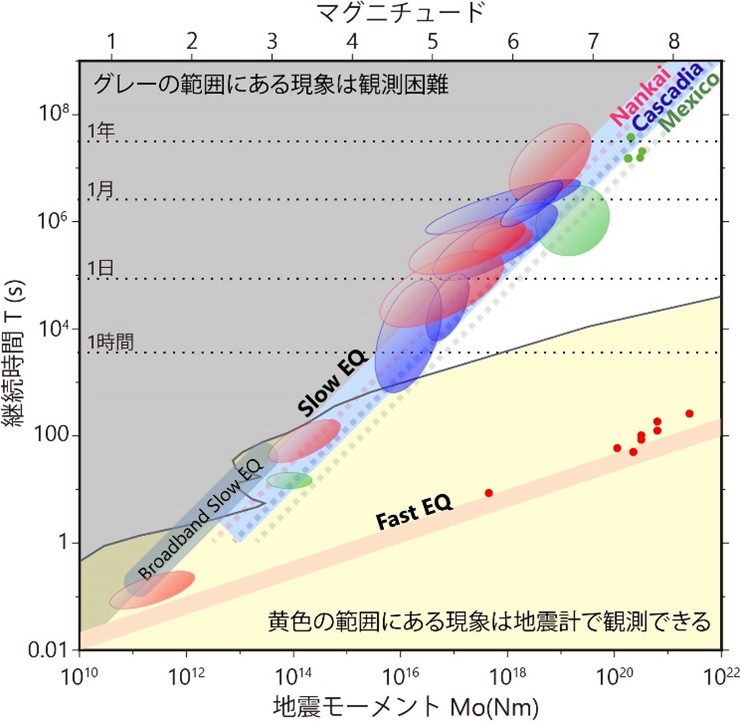
スロー地震のスケール法則(MoとTの関係)とファスト地震のスケール法則
発表概要
東京大学大学院理学系研究科の井出哲教授と、米国Stanford大学G. C. Beroza(ベローザ)教授は、スロー地震(注1)とファスト(普通の)地震の物理プロセスについての統一的な解釈を明らかにしました。21世紀初頭に発見されたスロー地震は、地震学、測地学のさまざまな観測によって、大きさの異なる現象が別の名前で呼ばれるなど、その全体像の把握が困難でした。2007年に同じ著者らは、「スロー地震のスケール法則」を提案し、異なる名前の現象が、単一の物理プロセスから生じている可能性を提起しました。
この提案は、世界の地震研究者間に論争を生み出し、そのスケール法則に対して、さまざまな異論が提出されました。一方で15年間の研究の蓄積によって、多様なスロー地震の定量的な評価が可能になりました。今回の論文は、この状況を整頓し、スケール法則に対する異論のほぼすべてが、不適切なデータ処理や数値計算の結果であること、一方で2007年には限定的だったスケール法則の証拠が、現在では1秒以下から1年以上の幅広い時間範囲で連続的に存在することを示しました。そしてスロー地震のスケール法則は、地球内部のさまざまな変形現象の、変形速度の上限を示す法則と解釈すべきであり、この法則に従わない普通の地震こそが、特殊な現象であるという視点の転換を提案しています。これは今後、地震活動の予測のための物理的モデルを構築するうえで重要な地震についての基礎的理解となります。
発表内容
〈研究の背景〉
2000年ごろから世界各地で、普通の地震とは異なる、奇妙な地震地殻変動現象が発見され、研究されるようになりました(図1)。
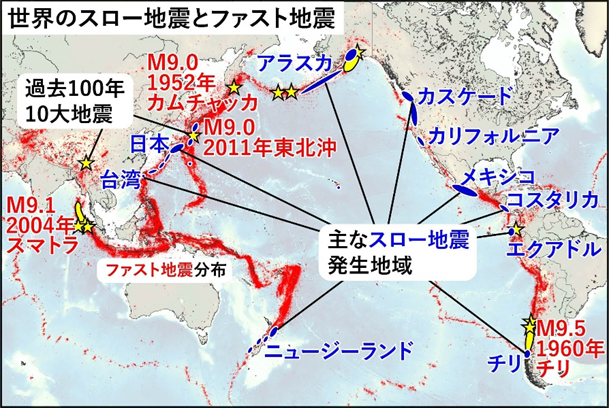
図1:世界のスロー地震(青)とファスト地震(赤)の発生地域および過去の10大地震(黄)
Slow-to-Fast地震学リーフレットより
この現象は、人間が感じない微弱な地面の揺れを引き起こしたり、地表面にわずか数センチメートルの地殻変動を引き起こしたりします。そのシグナルは微弱で、計測機器の観測限界に近く、ノイズが少ない場合に限って、いくつかの異なる周波数帯だけで観測されます。当初、異なる周波数帯のシグナルは、異なる現象のものだと考えられてきました。2007年に当研究グループは、これらのシグナルは同一の物理プロセス「スロー地震」から放出されているという仮説を立て、その支配法則である「スロー地震のスケール法則」を提唱しました。この法則では、地震の規模を表す地震モーメントMo(注2)という量が、現象の継続時間Tに比例します。一方、普通の地震のスケール法則では、MoはTの3乗に比例します。
地震の概念の拡大として注目されたこの仮説と法則ですが、当初の証拠は貧弱で、むしろ世界の研究者から、さまざまな批判を受けました。代表的なものとしては、スロー地震と普通の地震の中間的な現象があるはず、提案されたTの1乗ではなく、2乗もしくは3乗に依存する、もしくは途中で依存性が変化する、というさまざまな仮説です。それぞれ観測や数値計算からの「証拠」が提示されました。一方でスケール法則を支持する証拠も次第に蓄積し、新しい観測による直接的な証拠や、新しい解析手法による間接的な証拠が提示されました。しかしさまざまな説が乱立する状況は、混乱しているようにみえました。
〈研究の内容〉
一見混乱した状況を整頓し、スロー地震と普通の地震、もしくはファスト地震を統一的に説明することが、今回の研究の目的でした。まず混乱を避けるために、対象地域を研究の進んだ日本、米国・カナダ、メキシコの3地域に絞り、さまざまな「証拠」の検証を行いました。例えばNature誌に掲載された、MoがTの3乗に依存するという説は、不適切なデータ処理に基づくものであることを証明し、また同様に3乗則を主張した数値計算結果は、別の観測的な証拠と整合しないことを証明しました。また、提案されたスケール則と一見矛盾する証拠は、データセットのばらつきと範囲についての制約を考慮すると、矛盾どころか整合的であることを明らかにしました。何より15年間の探索をもってしても、スロー地震とファスト地震の中間的な現象は見つからなかったという事実が、両者が基本的に異なる現象であることを示しています。
一方で、スロー地震の多様性は、ファスト地震よりはるかに大きいことは明らかでした。多様な現象を、観測限界ぎりぎりで観測すると、必然的に大きなシグナルだけを検出することになります。2007年のスケール法則は、この最大値を制約する法則であると、再定義する必要がありました。この再定義と、近年の新しい観測事実をすべてまとめると、1秒以下から1年以上という幅広い時間スケールで、スロー地震のスケール法則の証拠が連続的に存在することが証明できます(図2)。これらの証拠によって、スケール法則に関する論争に終止符を打つことができたと考えています。
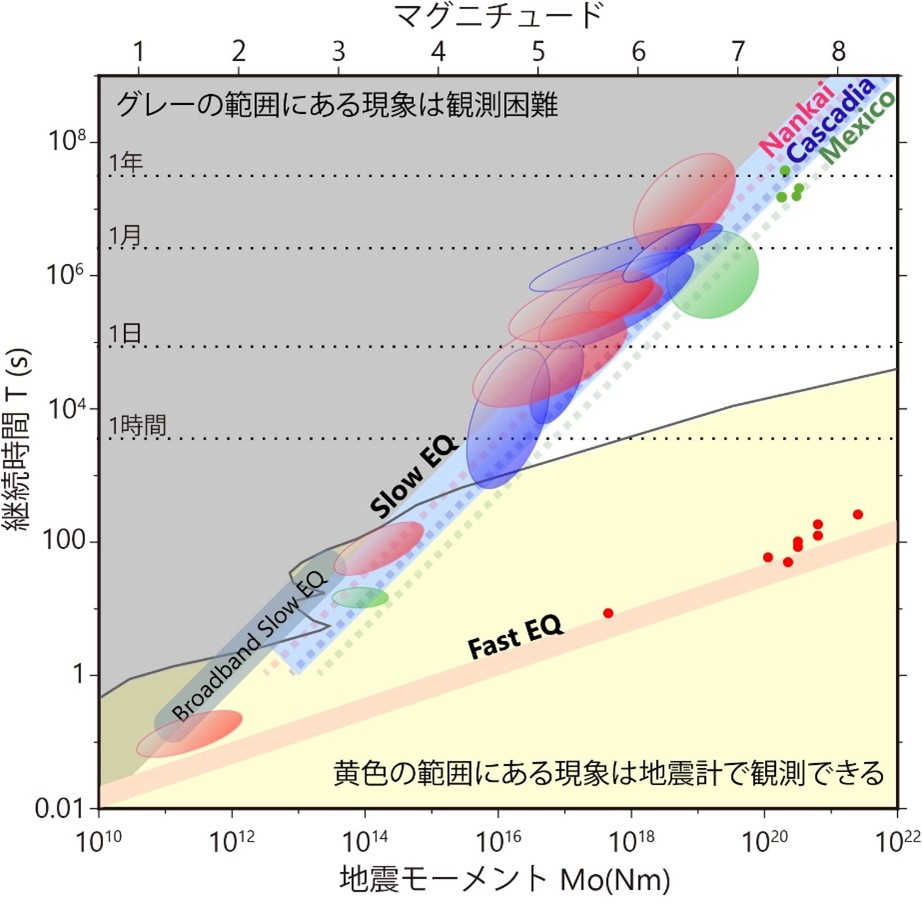
図2:スロー地震のスケール法則(MoとTの関係)とファスト地震のスケール法則
南海(日本)、カスケード(米国・カナダ)、メキシコのスロー地震の分布範囲をそれぞれ赤、青、緑の楕円で表す。ファスト地震のうち、特に継続時間が長いものを赤い点で示しているが、これらはスロー地震の分布からは大きく離れている。
スロー地震とファスト地震が異なる現象というためには、何がその違いを生み出しているかを説明することも必要です。2007年の段階では、この説明は困難でしたが、現在は確率過程モデルなどを用いて、スロー地震は拡散プロセスに支配された現象だと説明することができます。これは地震波動プロセスに支配されたファスト地震とは明らかな違いです。その違いのために、現象がより長く続く時に、スロー地震の大きさは、ファスト地震のように大きくなることができないのです(図3)。
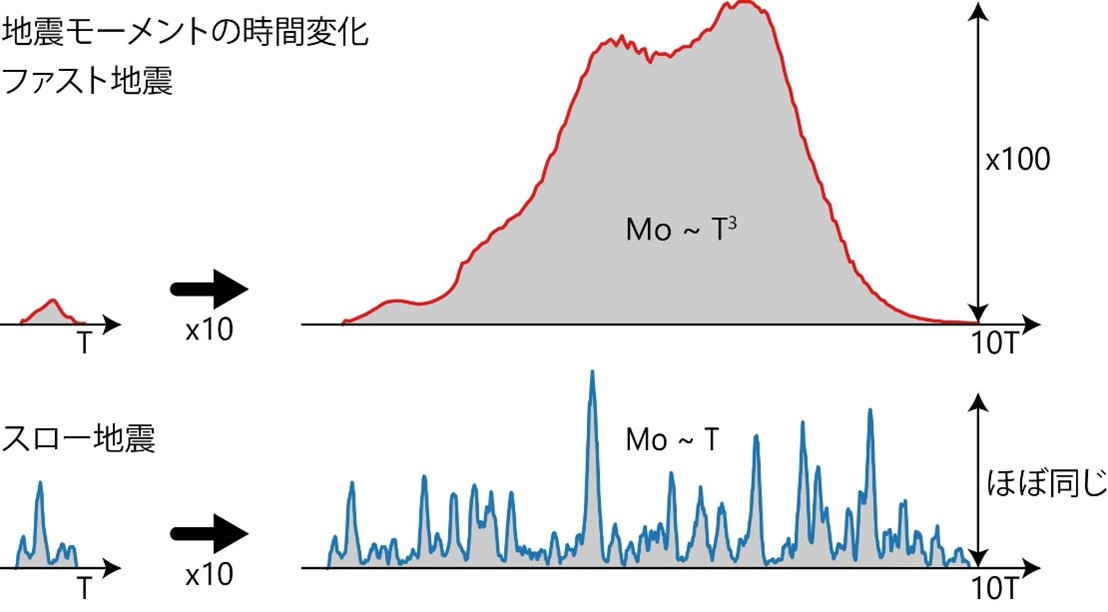
図2:スロー地震とファスト地震の大きくなりかたの違いの概念図
具体的に拡散している物理量が何か、については未解明なままですが、そもそも地球内部の変形の多くは拡散的なプロセスで進行しており、その点でスロー地震は変形現象としては、ありふれた現象といえるかもしれません。そのプロセスの速度限界を示すのが、スロー地震のスケール法則といえます。スロー地震が発見された当初、地震学者は、この異常な現象に着目し、その異常性を説明しようとしてきましたが、むしろスロー地震はありふれた拡散現象であり、それと異なる波動プロセスのファスト地震がむしろ異常な変形現象といえるのかもしれません。
〈今後の展望〉
発見から20年以上たち、スロー地震の社会的な認知度は、次第に高まっています。近年ではさまざまなメディアで取り扱われるなど、注目が高まる一方です。しかし、その基本的な物理プロセスの理解という意味では、前述のような一見混乱した状態にあったわけで、今回それを整頓できたことの意義は大きいと考えています。
将来の地震活動に対して定量的な予測を行ううえで、基本となる現象の正しい理解は重要です。現在は地震の理解と対策の転換期にあります。20世紀には、地球の内部には地震がおきていない定常な状態と、地震発生時という二つの状態しかないと考えられてきました。2017年まで運用されていた、我が国の地震対策も、この理解に基づくものだったと言えます。スロー地震の発見が、この考えを根本から変えましたが、それをどのように予測に取り入れていくか、まだ明瞭な指針はありません。例えば現在、国は南海トラフの巨大地震に備えるために、南海トラフ地震臨時情報を発出する可能性があります。その判断根拠の一つはスロー地震ですが、それを使ってどのような情報を出せるのか、専門家もまだわかりません。今回の成果は、今後適切なモデルを作って予測をし、対策を取る上で基盤的な認識となります。
論文情報
-
雑誌名 The Proceedings of the National Academy of Sciences (PNAS) 論文タイトル Slow Earthquake Scaling Reconsidered as a Boundary between Distinct Modes of Rupture Propagation
著者 Satoshi Ide and Gregory C. Beroza
研究助成
本研究は、科研費「Slow-to-Fast地震学(課題番号:21H05200)」、「震源の階層的固有性と広帯域性に基づく確率論的地震発生論の構築(課題番号:21H04505)」、災害の軽減に貢献するための地震火山観測研究計画の推進について(第2次)の支援により実施されました。
用語解説
注1 スロー地震
地震と同じような地下での断層(もしくはプレート境界)のすべり運動です。普通の地震が長くても数分しか続かないのに対して、スロー地震は数ヘルツの振動から、年単位の地殻変動まで、継続時間の異なる現象として観測されます。かつて異なる周波数(もしくは継続時間)の現象は、異なる現象と考えられてきました。代表的には、数ヘルツの振動は、テクトニック微動、数十秒のゆっくりした揺れは、超低周波地震、数日から数か月の地殻変動はスロースリップと呼ばれます。↑
注2 地震モーメントMo
地震の大きさの一つの表現で、地震時にすべった断層の面積とすべった量を掛け合わせた量。この常用対数を使って(モーメント)マグニチュードが計算されます。↑
からの記事と詳細 ( スロー地震と普通の地震(ファスト地震)は何が違うのか? - s.u-tokyo.ac.jp )
https://ift.tt/QuozmF8