全1355文字
量子コンピューターは量子の重ね合わせ状態を使って計算します。普通のコンピューターと量子版の足し算回路を比べてみましょう。足し算回路はコンピューターの基本的な回路の一つであり、これをたくさん組み合わせることでさまざまな演算処理を実現できます。このため、足し算回路の違いが、量子コンピューターと普通のコンピューターの違いを端的に表現しているわけです。なお、コンピューターが扱う数字は「0」と「1」だけから成る2進数なので、足し算回路も0と1だけの計算を実行します注1）。
注1）ここで紹介する足し算回路は、2進数の1桁分を計算する回路、いわゆる半加算器です。実際の足し算回路（全加算器）には桁の繰り上げを処理する回路も必要になります。
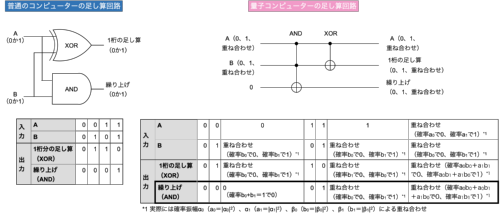
次の図を見てください。普通のコンピューターでは0と1のAND（論理積、2つの数字がどちらも1のときだけ1になる）を計算するANDゲートとXOR（排他的論理和、2つの数字が違うときに1になる）を計算するXORゲートを組み合わせて足し算回路を作ります。量子コンピューターでもANDゲートやXORゲートに相当する回路があって、それらを組み合わせることは同じです。なお、ゲートとはコンピューターの回路を構成する基本部品で、0や1を入力すると、ANDやXORといった論理演算を実行して、やはり0や1を出力する回路です。
普通のコンピューターと量子コンピューターの足し算回路
普通のコンピューターの足し算の回路（左側）と、それに対応する量子コンピューターの回路（右側）を比較した。量子コンピューターでも、古典コンピューターと同様なXORゲートやANDゲートを使う。ただし、データを送る線のつなぎ方や動作に違いがあるので、これらの回路は違った図形で表される。最大の違いは、0と1を重ね合わせた状態のデータを扱えることにある。
[画像のクリックで拡大表示]
量子コンピューター版の入力と出力を普通のコンピューター版と比べると、0や1を入力した場合は、普通のコンピューターと全く変わりません。両者の違いである重ね合わせの場合は、基本的に重ね合わせの状態が出力されます。
このように、量子コンピューターでは量子の重ね合わせの状態で計算をすると、複数の場合を同時に考慮した結果が、重ね合わさって出てきます。これによって複数の結果を1回の演算で導き出せるのです。
たった4つの計算を同時にできても大したことはないと思うかもしれません。しかし、量子コンピューターが扱える重ね合わせ状態の数は、回路の規模を大きくすることでどんどん増えていきます。それに応じて、同時に計算できる場合の数は爆発的に増加します。
重ね合わせ状態が1つの場合は2通り、2つの場合は4通りの計算ができたのは、前者ではあり得る状態が0、1という2種類、後者ではこの2種類を掛け算した2種類×2種類の合計4種類あったからです。
同様に、重ね合わせ状態がn個あると、全部の状態の組み合わせは2×2×2×…×2と、2をn回掛け算した分になります。つまり2のn乗（＝2n）です。この数はnが増えるに従って途方もない数に膨れ上がることは、連載の問題17でも説明した通りです。nが10だと1024、50では1000兆を超え、100になると1×1030以上もの状態がある、すなわちそれだけの数の計算を同時に実行できることになります。
このように量子コンピューターは指数的に大きな状態を取れるから速いのですが、測定すると1つの状態に収束してしまうので、当てずっぽうに計算しても欲しい状態が出る確率は指数的に小さくなります。並列に実行できる計算の数が指数関数的に増えることをうまく利用するアルゴリズムがあったときに、初めて量子コンピューターの計算回数を劇的に減らせます。
次回の一問一答
-
量子コンピューターのプログラムはどうやって書く？
からの記事と詳細 ( 量子コンピューターはなぜ問題を速く解ける？ - ITpro )
https://ift.tt/1X5SEvg
No comments:
Post a Comment