全1137文字
重ね合わせによってどんなに多くの計算が並列に実行できようと、その中から正解を取り出せなければ何の意味もありません。量子コンピューターのアルゴリズムには、望みの計算を実行するだけでなく、正解の確率を高める工夫が求められます。
そのイメージをつかむのに適しているのが、「グローバー(Grover)のアルゴリズム」です。データベースの高速な検索などに使えるため、量子検索アルゴリズムなどとも呼ばれます。このアルゴリズムが膨大な重ね合わせ状態の中から、どうやって正解を見つけるのかをざっくり説明します。
このアルゴリズムにできることは、N個の候補の中から特定の条件を満たす、M個の正解を見つけ出すことです。話を簡単にするため、ここではM=1、つまり正解は1つだけと考えます。単純にすべての候補が条件に合うかどうかを調べるとN回かかるところを、グローバーのアルゴリズムならおおむねNの平方根程度の回数で十分だとされます。Nが1万個の場合は100回程度、100万個あれば1000回程度の処理で正解が求まるわけです。
この問題を解く量子回路、すなわちアルゴリズムの概略を次の図に示しました。N=2nと仮定すると、量子ビットはn個用意すれば十分です。まずそれらをアダマールゲートに通すと、合計N(=2n)種類の状態を重ね合わせた状態になります。それぞれの状態が1~Nまでの答の候補に対応するわけです。もしこの時点で量子ビットを測定すると、正しい答が出る確率は当然ながら1/Nで、まず正解は見つかりません。
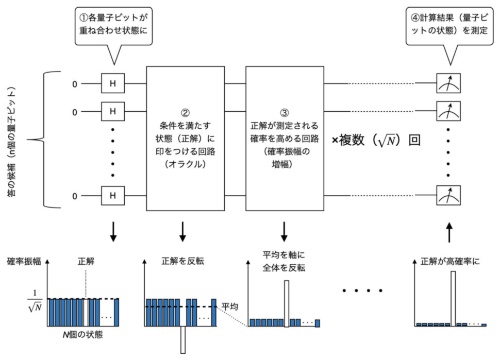
グローバーのアルゴリズム
グローバーのアルゴリズムでは、①まずn個の量子ビットを重ね合わせ状態にする。合計N(=2n)種類の状態が、等しい確率(1/N)で重ね合わさった状態になる(下側のグラフ)。グラフで1/√Nとなっているのは、グラフの縦軸は確率振幅を表しており、確率振幅は確率の平方根(ルート)になるからだ。②次に、正解の条件を満たす状態にだけ印をつける回路(オラクル)を、全ての量子ビットに適用する。具体的には、条件を満たす状態の確率振幅だけを反転して、マイナスの数字にする。③最後に、確率振幅の平均値を軸にして、全ての状態の振幅を反転させる。確率振幅の平均値は、①のときには1/√Nだが、②で正解を反転したので、1/√Nよりも小さい値になっている。これを軸に全体を反転すると、正解の確率振幅は大きく、それ以外の確率振幅は小さくなる。②と③の操作を何度も繰り返すと、④量子ビットを測定したときに正解が得られる確率が1に近づく。②と③の処理を√N回程度繰り返せば十分高い確率で正解を検出できるとされている。
[画像のクリックで拡大表示]
グローバーのアルゴリズムでは、無数にある重ね合わせ状態の中から、正解の条件を満たすものだけに印をつける「オラクル」と呼ばれる回路を使います。オラクルとは神のお告げという意味で、それだけで答えが分かってしまいそうですが、問題に応じて量子回路として実装できると見なされています。
その作り方は省略しますが、ここでは「そういうものがあるんだ」くらいに思ってください。次に、オラクルで印をつけた正解の確率が高まり、それ以外の確率は低くなるような操作を施します。この2つを繰り返すと、最終的に正解の確率が十分高くなるわけです1)。
詳しい説明は図のキャプションに譲りますが、図の下にあるグラフの中で正解(白棒)が次第に高くなり、それ以外の棒が下がっていく様子が、正しい答だけが高確率になっていく状況に対応しています。もちろん、最終的に正解が測定される確率は完全な1にはなりません。それでも、得られた結果を条件に当てはめてみれば正しいかどうかは確認できますし、万一間違っていた場合でも、もう一度測定すれば今度はほとんど確実に正解を得られるはずです。2度続けて外れる確率は非常に低くなるからです。
参考文献1) 「Week2: Groverのアルゴリズム」-
量子コンピューターのソフト開発はハードの存在が必須?
からの記事と詳細 ( 量子コンピューターはどうやって正解を導く? - ITpro )
https://ift.tt/PM2Grwe
No comments:
Post a Comment